Weshalb Sie das kombinatorische Testen nicht nur bei Software anwenden sollten

Testverfahren wie das kombinatorische Testen (z.B. das paarweise Testen) sind bei Software seit Jahrzehnten bekannt und in Normen wie der ISO 29119 beschrieben.

Viele Hersteller wenden diese Verfahren jedoch nicht einmal bei Produkten, die Software enthalten, angemessen an. Damit erhöhen sie zum einen die Risiken für Anwender und Patienten und zum anderen die Risiken für die Firma selbst: Denn Benannte Stellen fordern diesen Stand der Technik bei Audits und Zulassungen zunehmend ein.

A) Kombinatorisches Testen: Welches Dilemma Auditoren und Hersteller verstehen müssen

1. Die Pflicht, die Sicherheit nachzuweisen, bedeutet nicht, Fehlerfreiheit nachzuweisen

Gesetze und EU-Verordnungen wie die MDR und IVDR verpflichten Hersteller dazu, die Sicherheit, die Leistungsfähigkeit und den Nutzen ihrer Produkte nachzuweisen.

Viele Prüfer und Benannte Stellen leiten daraus die Forderung ab, dass der Hersteller nachzuweisen habe, dass das Produkt inklusive dessen Software fehlerfrei ist. Doch dieser Nachweis lässt sich nicht erbringen.

2. Vollständiges Testen ist unmöglich

Schon ein System wie ein Software-System oder eine Software-Komponente mit nur drei Eingängen, deren Werte ganze Zahlen von Null bis 32.000 annehmen können, bräuchte 32.000³ = 32.768.000.000.000 Testfälle.

Selbst bei 10.000 Testfällen pro Sekunde würde der Test über 100 Jahre laufen.

Dabei wäre selbst ein Test inakzeptabel, der für diese drei Eingabewerte nur eine Minute benötigt. Schließlich müssen in einem System zehntausende dieser Prüfungen durchgeführt werden.

Daraus folgt, dass solch ein System niemals zu 100 % getestet werden kann. Im obigen Beispiel sind nicht einmal 0,000001 % realistisch. Genau zu dieser Erkenntnis kommt auch die ISO 29119:

Es ist unmöglich, ein Softwaresystem 100 % zu prüfen, deshalb ist Prüfen nur eine Probenahme.

ISO 29119-1

3. Die Schlussfolgerungen

Daher sollten Sie mit Ihren Auditoren oder Prüfern immer klären, was diese unter einer 100%-Prüfung verstehen. Dass eine Prüfung aller Kombinationen von Eingangswerten unmöglich ist, hatten wir gerade dargelegt.

Allerdings ist auch der Umkehrschluss falsch, dass man sich das Testen gleich sparen könne, weil man nur einen verschwindend kleinen Teil der Kombinationen von Inputs prüfen kann.

Vielmehr müssen Hersteller gemäß dem Stand der Technik testen. Diesen Stand reflektieren Normen wie die ISO 29119.

So beschreibt die ISO 29119-4 im Kapitel 5.2.5 die „Combinatorial Test Design Techniques“ und im Kapitel 6.2.5 die „Combinatorial Test Design Technique Coverage“.

Das nächste Kapitel stellt die wichtigsten Aspekte dieses Verfahrens vor.

B) Wie kombinatorisches (z.B. paarweises) Testen funktioniert

1. Die Anzahl der gefundenen Fehler ist nicht proportional zur Anzahl der getesteten Parameter

Es hat sich gezeigt, dass es häufig nicht notwendig ist, alle möglichen Kombinationen von Eingabewerten zu testen. Vielmehr gelingt es, bereits mit wenigen Kombinationen (≤ 6) die meisten Fehler zu finden.

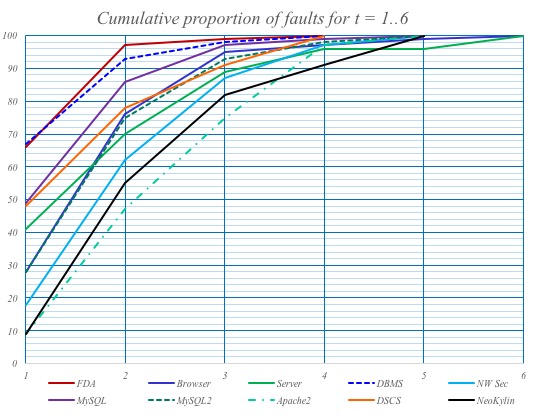
Das liegt daran, dass die meisten Fehler dadurch entstehen, dass die Verarbeitung einer Variablen nicht korrekt ist.

Etwas weniger Fehler treten dadurch auf, dass die Verarbeitung erst in Kombination von zwei oder mehr Variablen nicht spezifikationsgemäß erfolgt wie im folgenden Beispiel zu sehen.

Nur im Fall von Patienten, deren Gewicht über 120 kg und deren Laborwert unter 20 mg/dl beträgt, ist die Fehlerwirkung überhaupt sichtbar.

Die NIST formuliert diese Erkenntnis wie folgt:

Interaction Rule: Most failures are induced by single factor faults or by the joint combinatorial effect (interaction) of two factors, with progressively fewer failures induced by interactions between three or more factors.

Folglich sollten Hersteller einen Fokus auf das Testen der Kombination weniger Input-Werte legen. Die Herausforderung beim kombinatorischen Testen besteht also darin, mit möglichst wenigen Testfällen möglichst viele Kombinationen abzuprüfen.

2. Ableiten der Testfälle

Das kombinatorische Testen zählt zur Klasse der Blackbox-Testmethoden, denn es leitet die Testfälle nicht aus der Kenntnis des Innenlebens der Methode, der Komponente oder des Systems ab. Vielmehr besteht der Ansatz darin, Testfälle abzuleiten, in dem man systematisch verschiedene Input-Kombinationen bildet.

Weil man nicht alle Kombinationen testen kann, beschränkt man sich darauf, mit Inputs zu testen, die paarweise, zu dritt, zu viert usw. gruppiert werden.

Beispiel für paarweises Testen

In unserem Beispiel berechnet das System eine Behandlungsempfehlung auf Basis von fünf Inputs:

1. Geschlecht: männlich, weiblich
2. Diabetiker: kein Diabetes, Typ1-Diabetiker, Typ2-Diabetiker
3. Bestehende Medikamentenbehandlung: ja, nein
4. Allergiker: Keine Allergien, Hausstaubmilbenallergie, Pollenallergie
5. Altersklasse: Kind, Erwachsener

Um alle Kombinationen zu testen, bräuchte man 2 x 3 x 2 x 3 x 2 = 72 Tests. Das ist eine handhabbare Menge. Doch bei mehr Inputs (Variablen) oder einer größeren Anzahl an möglichen Variablenwerten wäre das nicht mehr der Fall.

Beim paarweisen Testen stellt man sicher, dass alle möglichen Kombinationen zweier Input-Werte getestet werden. Beispielsweise müssten für die beiden ersten Inputs (Geschlecht, Diabetiker) die Testfälle aus dem Kreuzprodukt des Vektors 1 (männlich, weiblich) und dem Vektor 2 (kein Diabetes, Typ1-Diabetiker, Typ2-Diabetiker) gebildet werden. Das führt zu sechs Testfällen.

Durch kluges Kombinieren gelingt es in unserem Beispiel mit fünf Inputs, die paarweisen Kombinationen mit nur neun Testfällen zu überprüfen:

Test Case	sex	diabetic	medicated	allergy	age
1	female	no	false	no	adult
2	male	no	true	dust	child
3	female	no	true	pollen	adult
4	male	type1	false	no	child
5	female	type1	true	dust	adult
6	male	type1	false	pollen	child
7	female	type2	true	no	child
8	male	type2	false	dust	adult
9	male	type2	true	pollen	adult

Sie finden in Tabelle 1 auch die eben erwähnten sechs Testfälle wieder, die die Kombination der Werte für „Geschlecht“ und „Diabetiker“ repräsentieren.

Das paarweise Testen benötigt in diesem Beispiel nur neun statt 72 Testfälle.

Beispiel für Testen von Dreierkombinationen

Beim Testen von Dreierkombinationen (3-way testing) gilt es, die möglichen Kombinationen von drei Input-Variablen zu prüfen. Bei den Variablen „Geschlecht“, „Diabetiker“, „Bestehende Medikamentenbehandlung“ wären das 2 x 3 x 2 = 12 Tupel.

Diese 12 Tupel sind in Tabelle 2 fett hervorgehoben.

Test Case No.	sex	diabetic	medicated	allergy	age
1	male	no	true	no	child
2	female	no	false	no	adult
3	male	no	false	dust	child
4	female	no	true	dust	adult
5	male	no	true	pollen	adult
6	female	no	false	pollen	child
7	male	type1	false	no	adult
8	female	type1	true	no	child
9	male	type1	true	dust	child
10	female	type1	false	dust	adult
11	male	type1	false	pollen	child
12	female	type1	true	pollen	adult
13	male	type2	true	no	adult
14	female	type2	false	no	child
15	male	type2	false	dust	adult
16	female	type2	true	dust	child
17	male	type2	true	pollen	child
18	female	type2	false	pollen	adult

Die Testfälle in dieser Tabelle enthalten auch alle anderen möglichen Kombinationen aus drei beliebigen Input-Variablen.

Das Testen von Dreierkombinationen benötigt in diesem Beispiel nur 18 statt 72 Testfälle.

3. Kombinatorisches Testen von Zustandsautomaten

Häufig treten Fehler nicht nur bei bestimmten Kombinationen von Eingabewerten auf, sondern auch dann, wenn Systeme nicht in der richtigen Reihenfolge bedient werden. Eine solche Reihenfolge könnte sein:

• A: Von Standby auf Betrieb schalten
• B: Selbsttest durchführen
• C: Behandlungsparameter einstellen
• D: Behandlung durchführen

Diese vier Ereignisse lassen sich in 4! = 24 verschiedenen Reihenfolgen kombinieren. Es wird klar, dass bei mehr Ereignissen sehr schnell eine kombinatorische Explosion der Testfälle folgt. Auch hier kann das kombinatorische Testen helfen:

Wenn man sich auf ein paarweises Testen der Reihenfolgen beschränkt, bleiben nur noch zwei Testfälle übrig:

Testfall	1. Ereignis	2. Ereignis	3. Ereignis	4. Ereignis
1	A	B	C	D
2	D	C	B	A

Jedes beliebige Paar an Ereignissen (z.B. (A,B) oder (C,D)) wird in jeder Reihenfolge überprüft.

Bei 50 Ereignissen reduziert sich die Anzahl der Testfälle von 3 x 10⁶⁴ radikal:

Anzahl Kombinationen	Anzahl notwendiger Testfälle
2	2
3	34
4	214

 

4. Coverage-Grade

Als Maß für die Vollständigkeit von Tests setzen Entwickler meist Coverage-Grade wie Statement Coverage (Anweisungsabdeckung) oder Branch Coverage (Zweigabdeckung) ein. Doch das sind Maße für das Whitebox Testing, die den Zugriff auf den Source Code bedingen und somit auch nur bei Software anwendbar sind.

Verhältnis von getesteten und möglichen Kombinationen

Für das kombinatorische Testen existieren mehrere dieser Abdeckungsgrade. Einer berechnet sich als das Verhältnis aus der Anzahl der getesteten Kombinationen und der Anzahl der existierenden Kombinationen von Input-Werte.

Im obigen Beispiel hatten wir beim paarweisen Testen neun von 72 Kombinationen getestet. Das entspricht ca. 12 %.

Dieses Maß ist nicht sehr hilfreich, da Abdeckungsgrade im Sub-Promille-Bereich eher die Regel als die Ausnahme sind.

„t-way Combination Coverage“

Hilfreicher ist das Abdeckungsmaß, das für n Variablen den Anteil der t-fachen (z.B. paarweisen) Kombinationen prüft, für die alle Kombinationen überprüft wurden.

Reduzieren wir zur Illustration unser Beispiel von oben auf drei Inputs:

• Geschlecht: männlich, weiblich
• Diabetiker: kein Diabetes, Typ1-Diabetiker, Typ2-Diabetiker
• Bestehende Medikamentenbehandlung: ja, nein

Es gibt beim paarweisen(!) Testen somit folgende Kombinationen, die überprüft werden müssten

• Geschlecht – Diabetiker
• Geschlecht – Bestehende Medikamentenbehandlung
• Diabetiker – Bestehende Medikamentenbehandlung

Angenommen, man hätte wie folgt getestet:

Test Case	sex	diabetic	medicated
1	male	no	true
2	female	no	false
3	male	no	false
4	female	no	true
5	male	no	true
6	male	type1	false

Ergebnis:

• Die 1. Kombination (Geschlecht – Diabetiker) ist nicht vollständig getestet.
• Die 2. Kombination (Geschlecht – Bestehende Medikamentenbehandlung) ist komplett getestet (fett hervorgehoben).
• Die 3. Kombination (Diabetiker – Bestehende Medikamentenbehandlung) ist nicht vollständig getestet

Es wurde also nur ein Drittel der Kombinationen vollständig getestet; der Abdeckungsgrad beim paarweisen Testen liegt bei 33 %.

Beim 3-way testing wären es 0 %, denn das hätte bedingt, dass die Testfälle die drei Variablen in allen drei Kombinationen abgedeckt hätten.

Weitere Coverage-Grade

Die ISO 29119-4 beschreibt weitere Coverage-Grade. Sie sei daher zum Studium empfohlen, auch wenn die Ausführungen sehr kompakt sind.

C) Die 7 Vorteile des kombinatorischen Testens

1. Vorteil: Sichere Produkte entwickeln

Viele Produktfehler, die z.T. zu gravierenden Risiken für Patienten, Anwender und Dritte geführt haben, hätten durch ein systematisches Testen entdeckt werden können, ja entdeckt werden müssen.

Das kombinatorische Testen ist eine sehr leistungsfähige Methode,

• um Testfälle abzuleiten, die eine besonders hohe Wahrscheinlichkeit haben,
• solche Fehler zu entdecken und damit
• die Risiken zu minimieren, d.h. die Sicherheit des Produkts zu erhöhen.

2. Vorteil: Entwicklungsaufwand verringern

Gleichzeitig hilft das kombinatorische Testen dabei, der kombinatorischen Explosion möglicher Testfälle Herr zu werden und die Dauer für Tests zu minimieren.

Das ermöglicht es, diese Tests als Regressionstests parallel zum Entwicklungsprozess regelmäßig laufen zu lassen und dadurch Fehler früh zu entdecken. Das wiederum senkt den Aufwand für die Fehlerbehebung und damit Entwicklungsdauer und -kosten.

3. Vorteil: Tool-Unterstützung

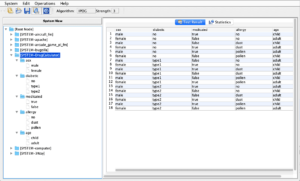
Die Algorithmen zum Ableiten der Testfälle sind komplex. Allerdings sind diese längst in Software-Werkzeugen implementiert. Das ACTS-Tool der NIST gibt es sogar zum kostenlosen Download.

ACTS steht für Automated Combinatorial Testing for Software.

4. Vorteil: Universelle Anwendbarkeit – nicht nur bei Software

Das kombinatorische Testen ist nicht auf Software beschränkt. Ein Input ist ein Input: Ob dies ein Übergabewert einer Methode oder die Stellung eines Schalters an einem Gerät ist, spielt keine Rolle.

Daher sollten Hersteller von den Vorteilen dieses Verfahrens nicht nur bei Software Gebrauch machen, auch wenn das kombinatorische Testen dort einen besonderen Schub erfährt:

Beim Testen von Machine-Learning-Modellen, deren Innenleben in gewisser Weise eine Blackbox darstellt, drängt sich das kombinatorische Testen gerade zu auf.

Das Johner Institut setzt auch bei der Validierung von Machine-Learning-Bibliotheken auf diese Methoden.

Melden Sie sich, falls Sie mehr darüber erfahren wollen und an Unterstützung interessiert sind.

5. Vorteil: Voraussetzung, um Produkte in den Verkehr zu bringen

Die Publikationen enthalten wertvolle Hinweise darauf, mit welcher Wahrscheinlichkeit Fehler in Software vorhanden sind.

Das (falsche) Argument, dass man bei Software von einer Wahrscheinlichkeit von 100 % ausgehen müsse, ist damit widerlegt. Denn bei einer 100%igen Wahrscheinlichkeit dürften die meisten Produkte nicht in den Verkehr gebracht werden.

6. Vorteil: Steuerungselement für Entwicklungsleitung und QS

„Habt Ihr nicht getestet?“ lautet regelmäßig die Frage des Produktmanagements, der Entwicklungsleitung oder der Qualitätssicherung, wenn ein Software-Fehler erst im Markt entdeckt wurde.

Das ist die falsche Frage. Die Frage müsste lauten: „Habt Ihr ausreichend getestet?“ Für dieses „ausreichend“ bedarf es einer quantitativen Bewertung. Das kombinatorische Testen liefert neue Abdeckungsgrade, mit deren Hilfe diese Frage quantitativ beantwortet werden kann.

Diese Abdeckungsgrade eigenen sich daher sowohl für Vorgaben im Software-Entwicklungsplan als auch als Kriterien bei der Software-Freigabe.

7. Vorteil: Argumentationshilfe mit Behörden und Benannten Stellen

Die quantitative Bewertung ist zudem bei der Argumentation mit Benannten Stellen und Behörden sehr hilfreich. Normen wie die ISO 29119 beschreiben den Stand der Technik beim Testen von Software. Dazu zählt seit über 20 Jahren auch das kombinatorische Testen.

Hersteller und Behörden bzw. Benannte Stellen sollten mit Hilfe dieses Ansatzes Einigung bei den folgenden Fragen erzielen:

• Was ist der Stand der Technik beim Software-Testing?
• Wie kann man die Wahrscheinlichkeit von Fehlern abschätzen?
• Wie vollständig hat der Hersteller getestet?
• Hat er dabei das Bestmögliche getan, um die Sicherheit seines Produkts zu gewährleisten?

Eine gemeinsame Sichtweise zu diesen Fragestellungen bedeutet ein gemeinsames Verständnis von den Voraussetzungen für eine „Zulassung“. Genau daran hapert es regelmäßig.

D) Zusammenfassung und Fazit

a) Vorteile nutzen

Die Vorteile des kombinatorischen Testens liegen auf der Hand. Daher sollten Hersteller das kombinatorische Testen zum festen Teil ihrer Entwicklungspläne machen. Es ist Stand der Technik.

Gleichzeitig müssen sich Benannte Stellen und Behörden, die von Herstellern eine 100%-Prüfung (im Sinne einer Prüfung aller möglichen Kombinationen von Eingangswerten) verlangen, die Frage gefallen lassen, ob ihr eigenes Wissen „State of the Art“ ist. Solche unsinnigen Forderungen haben wir leider schon erlebt.

b) Herausforderungen kennen

Das kombinatorische Testen ist nicht die Lösung aller Probleme:

• Es ist kein Ersatz für andere Blackbox-Testmethoden, sondern eine Ergänzung. Beispielsweise wird es nur in Kombination mit Äquivalenzklassen-basiertem Testen gelingen, mit numerischen Inputs umzugehen.
• Die Tools helfen beim Ableiten von Testfällen, aber nicht beim Spezifizieren von Sollwerten. Dazu bedarf es weiterer Methoden und Werkzeuge (sog. Test-Orakel).
• Tests sind und bleiben ein Mittel, um Fehler zu finden. Sie sind kein Mittel dafür, die Korrektheit von Systemen zu beweisen.

Auch die besten Tests ersetzen keine konstruktive Qualitätssicherung in Form von z.B. Entwicklungsprozessen, einem systematischen Requirements Engineering oder einer professionellen Modellierung von Architekturen.

Professionelle Tests sind daher nur eine notwendige, aber keine hinreichende Voraussetzung für die Zulassung von Medizinprodukten.

Der Einsatz von kombinatorischen Tests zählt zum Arsenal professioneller Tester.

---

Das Johner Institut unterstützt Medizinproduktehersteller dabei, Software IEC-62304-konform zu entwickeln. Das betrifft Stand-alone-Software wie Apps und IT-Systeme ebenso wie Gerätesoftware und Machine-Learning-Komponenten.

Melden Sie sich gleich (z.B. über unser Webformular). Die Software-Experten des Johner Instituts freuen sich auf Sie.

Dank an Kai Haase für Unterstützung bei der Recherche

Änderungshistorie

• 2021-04-13: Link mit weiterführenden Informationen zu Testwerkzeugen ergänzt